Инвертирование матриц
Инвертирование матриц
В математике матриц нет аналога операции деления, но зато есть мультипликативная операция инвертирования. Приведенный ниже список обобщает важные особенности инвертирования:
Инвертировать можно только квадратные матрицы, так что когда мы говорим об инвертировании матрицы, подразумевается, что мы имеем дело с квадратной матрицей.
В результате инвертирования матрицы M размером n× n получается матрица размером n × n, которую мы будем обозначать M-1.
Не всякую квадратную матрицу можно инвертировать.
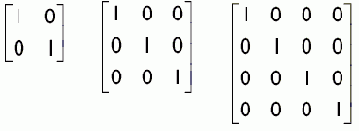
Если перемножить исходную и инвертированную матрицы, получится единичная матрица: MM-1 = M-1M = I. Обратите внимание, что в случае перемножения исходной и инвертированной матриц операция умножения матриц коммутативна.
Инверсия матриц применяется для нахождения искомой матрицы в уравнениях. Для примера возьмем выражение p' = pR и предположим, что нам известны p' и R, а требуется найти p. Сначала вычислим R-1 (подразумевается, что эта матрица существует). Получив R-1 можно вычислить p по следующему алгоритму: